Análisis de Datos de Salida de la Simulación para un Solo Sistema

---

 ¿Por qué es importante el análisis de resultados en simulación?

• 🎯 ¿Qué pasa si no analizamos correctamente?
  • Una sola corrida → puede dar resultados engañosos
  • Las salidas de simulación son variables aleatorias
  • Debemos estimar parámetros (como la media) usando estadística
  • Muchos estudios se enfocan en programar el modelo y descuidan el análisis-
• 📊 La simulación NO da una respuesta exacta
  • Estimamos, no determinamos
  • Cada réplica puede dar un resultado distinto
  • El análisis permite cuantificar el error de muestreo
• 📌 Necesitamos:
  • Múltiples réplicas independientes
  • Intervalos de confianza
  • Comparaciones estadísticas

---

Principios clave del análisis de salida

1. Variabilidad y replicación
   • Cada corrida genera un resultado distinto → ¡hay que repetir!
   • Simulamos con distintas semillas aleatorias
2. Estimaciones con error
   • Usamos medias muestrales, varianzas y proporciones
   • Aplicamos intervalos de confianza para cuantificar la incertidumbre
3. Tipos de simulación
   • Terminante: tiene un final natural (ej. banco que cierra)
   • No terminante: análisis en estado estable (ej. red de datos)

---

Conclusion

Sin análisis estadístico, no hay simulación confiable.

---

Independencia entre corridas (replicas)

[Ejemplo 9.1] Consideremos un banco con 5 cajeros y una cola, el cual abre a las 9:00 AM y cierra a las 5:00 PM, pero permanece abierto hasta que todos los clientes presentes en el banco a las 5:00 PM hayan sido atendidos. Supongamos que los clientes llegan según un proceso de Poisson con una tasa promedio de 1 cliente por minuto; es decir, los tiempos entre llegadas son independientes e idénticamente distribuidos (IID) con distribución exponencial y media de 1 minuto. Los tiempos de servicio son variables aleatorias exponenciales (IID) con media de 4 minutos. La siguiente tabla muestra estadísticas típicas obtenidas en 10 réplicas independientes de la simulación del banco, asumiendo que no hay clientes presentes al inicio.

---

Note cómo los resultados de diferentes réplicas difieren entre sí, por lo que una sola corrida no proporciona la respuesta real del sistema.

---

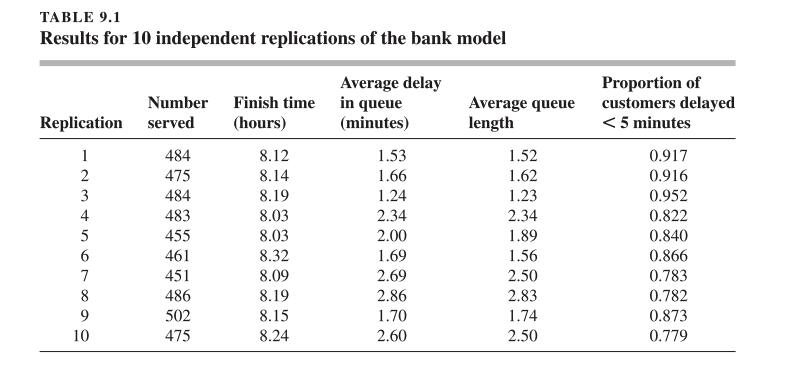
De los datos en la tabla se puede afirmar que los resultados de cada corrida (filas) son independientes entre sí, debido a que en cada corrida se utiliza una secuencia diferente de números aleatorios, aunque el modelo y las condiciones iniciales sean idénticos.

Dentro de una misma corrida, los datos observados no son necesariamente independientes ni idénticamente distribuidos (por ejemplo, el tiempo de espera del primer cliente podría influir en el del segundo cliente).

Este concepto de independencia entre corridas es crucial porque permite aplicar técnicas estadísticas estándar, como intervalos de confianza y pruebas estadísticas, sobre cada columna para inferir características reales del sistema simulado.

---

Comportamiento transitorio y de estado estable en los procesos estocásticos

1. Comportamiento transitorio
   • Corresponde a la fase inicial de operación del sistema.
   • Está fuertemente influenciado por las condiciones iniciales.
   • Durante esta fase, la distribución de probabilidad de las variables aleatorias cambia con el tiempo.
   • Ejemplo clásico: un sistema de colas que comienza vacío; las primeras observaciones no reflejan el comportamiento típico del sistema.

📌 Importancia: Si se incluyen datos transitorios en el análisis sin considerar su efecto, se puede obtener un sesgo en la estimación de las métricas del sistema.

---

2. Comportamiento en estado estable
   • Se alcanza después de un “tiempo suficientemente largo” de operación.
   • Las distribuciones de las variables se estabilizan y se vuelven aproximadamente independientes del tiempo.
   • El sistema entra en equilibrio estadístico: la probabilidad de estar en un cierto estado ya no depende del instante en que se observe.

🧠 En términos probabilísticos:

Si $L(t)$ es la longitud de la cola en el tiempo $t$, entonces: $P(L(t)=n)\to P_n\text{para }t\to \infty$

---

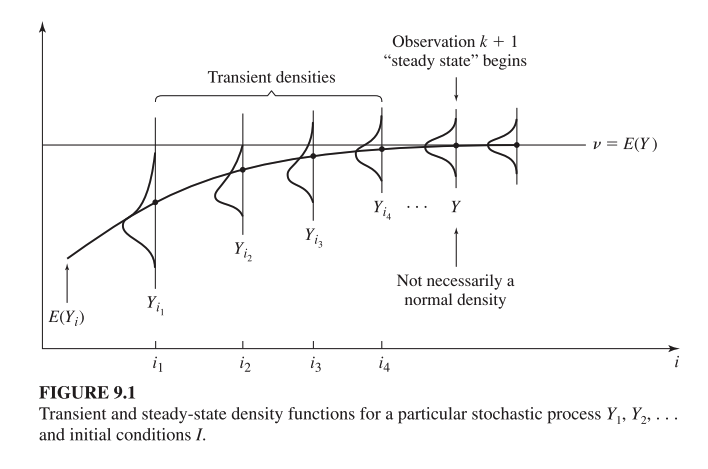
La figura 9.1 ilustra cómo evoluciona la distribución de probabilidad de una variable aleatoria de salida $Y_i$ en una simulación a medida que avanza el tiempo o el número de observaciones $i$.

• Cada curva $Y_i$ representa la densidad de probabilidad de la variable de salida en la observación $i$, o después de $i$ unidades de tiempo.
• Las primeras curvas (como $Y_1$, $Y_2$) reflejan el comportamiento transitorio, influenciado por las condiciones iniciales.
• Las curvas posteriores se van acercando a una forma estable, que corresponde a la densidad de probabilidad en estado estacionario

---

3. Procesos covariante-estacionarios
   • En estado estable, el proceso puede tratarse como covariante-estacionario, lo cual significa que sus propiedades estadísticas como la media y la varianza se mantienen constantes a lo largo del tiempo.

---

4. No todos los sistemas alcanzan estado estable., algunos procesos estocásticos:
   • Nunca alcanzan equilibrio (se quedan en fase transitoria indefinidamente),
     • Ejemplo: un sistema de colas con sobrecarga (ρ > 1)
   • O tienen comportamientos cíclicos o periódicos.
     • Ejemplo: Fábrica con turnos de producción cíclicos

---

5. Distribución límite
   • A medida que el tiempo avanza, la distribución de las variables aleatorias de salida se aproxima a una distribución límite o de estado estable F(y), independientemente de las condiciones iniciales I.
   • Sin embargo, la velocidad de convergencia a esta distribución sí depende de las condiciones iniciales.

---

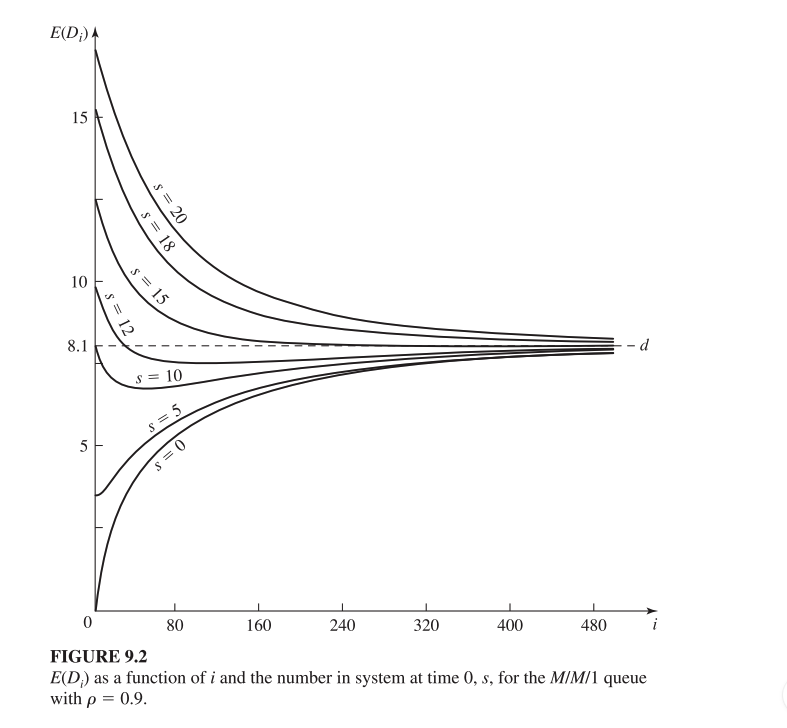
La figura 9.2 muestra cómo cambia el valor esperado del tiempo total en el sistema $E(D_i)$ para el cliente $i-\acute{e}simo$ en una cola M/M/1 a medida que el número de clientes observados $i$ aumenta.

La velocidad de convergencia depende de las condiciones iniciales:

• Si el sistema empieza vacío (s = 0), el tiempo en sistema inicia bajo y sube.
• Si empieza muy cargado (s = 20), los primeros clientes esperan mucho, pero el valor desciende con el tiempo

---

📌 Implicaciones para simulación

• Es fundamental identificar y remover el período transitorio antes de analizar datos en simulaciones no terminantes.
• Para eso se utilizan métodos como:
  • Descartar las observaciones iniciales (“warm-up period”),
  • O iniciar el sistema desde una condición representativa del estado estable.

---

Tipos de simulación en cuanto al análisis de salida

La forma en que se debe diseñar y analizar una simulación depende del tipo de simulación en cuestión. Existen dos tipos principales:

1. Simulación Terminante (Terminating Simulation)
2. Simulación No Terminante (Nonterminating Simulation)

---

Simulación Terminante (Terminating Simulation)

• 📌 Características:
  • Tiene un evento natural que determina el fin de la simulación (ej. el banco cierra, termina una campaña, se alcanza un objetivo).
  • Se usa cuando el período simulado es finito y relevante para el estudio.
  • Las condiciones iniciales suelen ser representativas de la realidad (ej. sin clientes al inicio del día).
• 📊 Ejemplos:
  • Un banco que abre a las 9:00 y cierra a las 17:00.
  • Una línea de ensamblaje que se reinicia cada jornada.
• 🧠 Implicación para el análisis:
  • Se realizan múltiples réplicas independientes.
  • Las medidas de salida (como el tiempo de espera promedio) son variables aleatorias IID.
  • Se pueden aplicar directamente técnicas de estimación e intervalos de confianza sobre estas réplicas.

---

Simulación no terminante (Nonterminating Simulation)

• 📌 Características:

  • No tiene un final natural evidente.
  • El interés está en estudiar el comportamiento a largo plazo o en estado estable.
  • Es importante eliminar el efecto de las condiciones iniciales (fase transitoria).

• 🧠 Consideraciones especiales:

  • Puede requerirse un período de calentamiento (warm-up).
  • Se deben aplicar técnicas estadísticas que consideren la correlación entre datos (ya que no son IID)

---

🧩 Subtipos de métricas en simulaciones no terminantes:

1. Parámetros en estado estable
   • Ej. tiempo promedio en cola después de estabilización.
2. Parámetros de ciclo en estado estable
   • Ej. producción por turno, rendimiento por día en sistemas cíclicos.
3. Otros parámetros
   • Ej. tiempo esperado hasta que ocurra un evento poco frecuente.

---

Tipo de simulación con respecto al análisis de salida

---

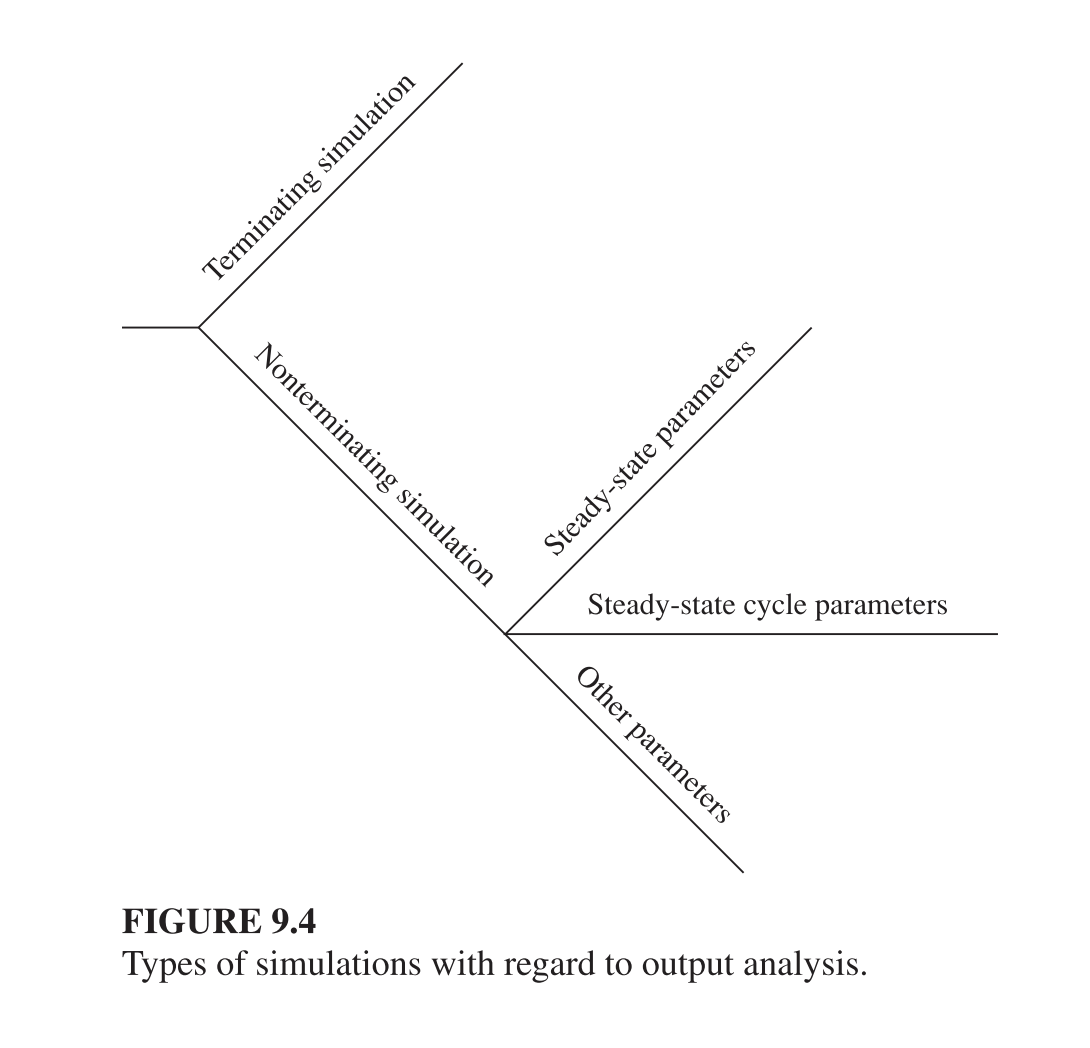
🧠 Conclusión clave:

La forma en que se deben recolectar y analizar los datos de salida depende de si el sistema tiene un punto natural de terminación o si requiere estudiar su comportamiento a largo plazo.

La clasificación terminante vs. no terminante es fundamental para aplicar correctamente los métodos estadísticos y evitar errores en la interpretación de resultados.

---

Análisis Estadístico para Simulaciones Terminantes

• ¿Qué caracteriza una simulación terminante?**
  • Existe un evento natural E que define el final de cada réplica (por ejemplo, cierre del banco, fin de una campaña).
  • Todas las réplicas se inician bajo las mismas condiciones iniciales, pero con diferentes secuencias de números aleatorios.
  • Cada réplica produce una medida de desempeño $X_j$ (por ejemplo, tiempo de espera promedio diario), que se modela como una variable aleatoria.

---

• Supuestos clave:

  • Las salidas $X_1,X_2,\dots ,X_n$ de las $n$ réplicas son independientes e idénticamente distribuidas (IID).
  • Este supuesto permite usar técnicas estadísticas clásicas como:
    • Estimaciones puntuales,
    • Varianza muestral,
    • Intervalos de confianza.

• 📊 Ejemplos de variables de salida $X_j$:

  • Tiempo promedio de espera en el día $j$ en un banco.
  • Tasa de pérdida de paquetes en una red simulada durante la réplica $j$.

---

Análisis Estadístico para Simulaciones Terminantes

NOTE

El análisis para simulaciones terminantes se basa en realizar múltiples réplicas independientes, tratar las métricas de salida como variables aleatorias IID, y aplicar estadística inferencial para estimar valores poblacionales como la media o proporciones.

---

Estimación de la media

• Se realizan $n$ réplicas independientes de la simulación, todas iniciadas con las mismas condiciones, pero con diferentes semillas aleatorias.
• Cada réplica produce un valor $X_j$, representando una métrica de salida (por ejemplo, el tiempo de espera promedio diario).
• Estas $X_j$ se consideran variables aleatorias IID (independientes e idénticamente distribuidas).

📊 Estimador puntual de la media:

La media muestral se define como:

$\bar{X}(n)=\frac{1}{n}{\sum }_{j=1}^n{X}_j$

Este valor es un estimador insesgado del valor esperado $\text{m}$ = E(X)$.

---

📐 Intervalo de confianza para $\mu$ :

Como el verdadero valor de \mu es desconocido, se construye un intervalo de confianza del $100(1-\alpha )$ %:

$\bar{X}(n)\pm t_{n-1,1-\alpha /2}\sqrt{\frac{S^2(n)}{n}}$

Donde

• $S^2(n)$ es la varianza muestral, calculada sobre los $X_j$,
• $t_{n-1,1-\alpha /2}$ es el valor de la distribución t de Student con $n-1$ grados de libertad.

---

[! INTEPRETACION] Con un nivel de confianza del $100(1-\alpha )$ %, podemos decir que el verdadero valor esperado $\mu$ se encuentra dentro del intervalo calculado. Este análisis nos permite tomar decisiones informadas a partir de los resultados de simulación, considerando la incertidumbre estadística asociada a los datos aleatorios.

---

Ejemplo de Estimación de la Media paso a paso

Supongamos que queremos estimar el valor esperado ($\mu$) del tiempo de espera promedio de un cliente durante el día, usando los datos de la Tabla 9.1 con un intervalo de confianza del 90%, basado en 10 réplicas de una simulación terminante.

Tiempos de espera promedio por réplica $(X_j)$ (en minutos):

1.53, 1.66, 1.24, 2.34, 2.00, 1.69, 2.69, 2.86, 1.70, 2.60

---

✏️ Paso 1: Calcular la media muestral $\bar{X}(10)$

$$\bar{X}(10)=\frac{1}{10}(1.53+1.66+\dots +2.60)=2.03\text{minutos}$$

---

✏️ Paso 2: Calcular la varianza muestral $S^2(10)$

Formula para la varianza muestral:

$S^2(n)=\frac{1}{n-1}{\sum }_{j=1}^n{\left(X_j-\bar{X}(n)\right)}^2$

Sustituyendo los valores en la formula: $S^2(10)=\frac{1}{10-1}{\sum }_{j=1}^{10}(X_j-2.03{)}^2=\frac{1}{9}\left[{\sum }_{j=1}^{10}(X_j-2.03{)}^2\right]$

Resultado de la varianza muestral:

$$S^2(10)=0.31$$

---

✏️ Paso 3: Determinar el valor $t_{9,0.95}$

• Queremos un intervalo con 90% de confianza, lo que implica:

  $$\alpha =0.10\Rightarrow 1-\alpha /2=0.95$$

• Buscamos el valor de t en la tabla de t de Student con $n-1=9$ grados de libertad:

---

$$t_{9,0.95}\approx 1.833$$

Tablas de t-student

---

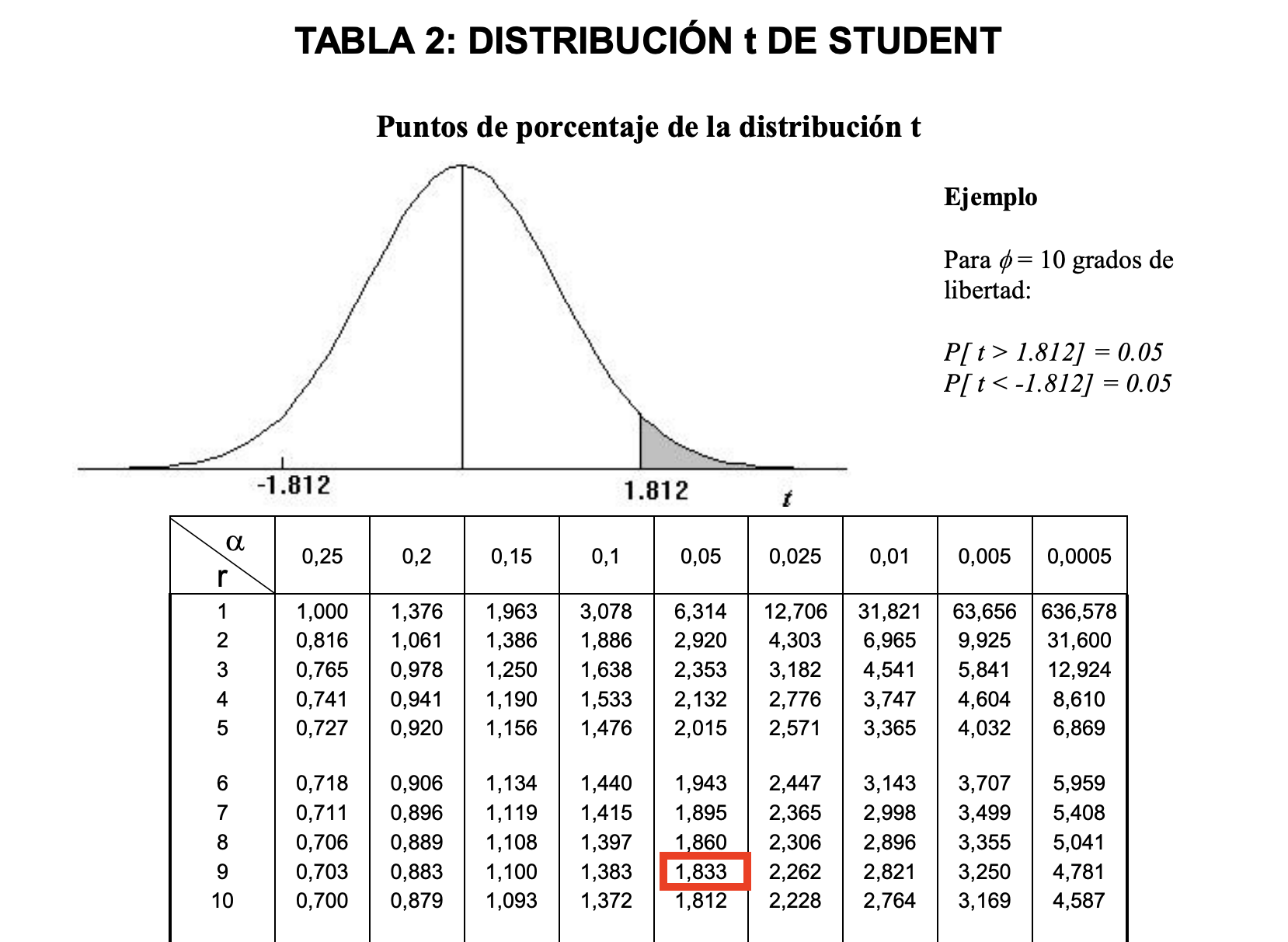
TIP

✅ Para un 90% de intervalo de confianza, busca el valor de t en la columna donde $\alpha =0.05$.

---

✏️ Paso 4: Calcular el error estándar y el intervalo de confianza

$$\text{Error estaˊndar}=\sqrt{\frac{S^2(10)}{10}}=\sqrt{\frac{0.31}{10}}=\sqrt{0.031}\approx 0.176$$ $$\text{Margen de error}=t\cdot \text{Error estaˊndar}=1.833\cdot 0.176\approx 0.32$$

---

✅ Resultado final

$$\mu \in \bar{X}(10)\pm 0.32=2.03\pm 0.32$$

Intervalo de confianza del 90%:

$$[1.71,2.35]\text{minutos}$$

---

📌 Interpretación

Podemos decir con un 90% de confianza que el tiempo de espera promedio diario de un cliente en el banco está entre 1.71 y 2.35 minutos, basado en las 10 réplicas simuladas

---

📘 Ejercicio: Estimación del tiempo promedio de espera en una sala de tren

🎯 Objetivo:

Aplicar el método de estimación de la media e intervalo de confianza usando datos de una simulación terminante.

🚉 Contexto del problema:

Una estación de tren regional abre sus puertas todos los días a las 6:00 a.m. y atiende pasajeros hasta las 10:00 a.m.. Durante ese período, los pasajeros llegan a la sala de espera según un proceso de Poisson con una tasa promedio de 1 pasajero cada 2 minutos.

El tren llega cada 30 minutos y se lleva a todos los pasajeros que estén esperando. El tiempo de espera de cada pasajero se mide desde su llegada hasta el momento en que aborda un tren.

Se desea estimar el tiempo promedio de espera de un pasajero durante una jornada.

---

🧪 Simulación:

Un estudiante simula este sistema usando un modelo computacional, realizando 10 réplicas independientes, cada una representando una jornada (de 6:00 a 10:00 a.m.).

Al final de cada réplica, obtiene el tiempo de espera promedio diario de los pasajeros atendidos ese día.

Los resultados en minutos son:

4.2, 3.9, 4.8, 5.1, 4.3, 4.0, 4.7, 5.3, 4.4, 4.6

---

📋 Instrucciones:

1. Calcular la media muestral $\bar{X}(n)$ de los tiempos de espera promedio.
2. Calcular la varianza muestral $S^2(n)$.
3. Determinar el valor $t_{n-1,1-\alpha /2}$ correspondiente a un 90% de intervalo de confianza.
4. Calcular el error estándar y construir el intervalo de confianza.
5. Interpretar el resultado: ¿Qué significa ese intervalo en el contexto del problema?

---

📌 Pregunta de reflexión:

• Comparar con un escenario donde el tren llega cada 15 minutos. ¿Cómo cambiaría el tiempo de espera esperado?

---

Precisión relativa y número de réplicas necesarias

En simulaciones terminantes, queremos estimar la media $\mu$ de una métrica de interés (por ejemplo, tiempo promedio de espera) con una precisión deseada y un nivel de confianza específico.

Pero… ¿cuántas réplicas necesitamos para lograr esa precisión?

Precisión relativa

La precisión relativa $g$ representa el margen de error permitido en proporción a la media estimada:

$g=\frac{\text{margen de error}}{\bar{X}(n)}$

🧠 Por ejemplo, si quieres que tu estimación esté dentro de un 10% del valor real, entonces $g=0.10$.

---

¿Cómo calcular el número de réplicas necesarias?

Se usa la fórmula:

$$n_r^{\ast }(g)={\left(\frac{t_{n-1,1-\alpha /2}\cdot \sqrt{S^2(n)}}{g\cdot \bar{X}(n)}\right)}^2$$

Donde:

• $\bar{X}(n)$: media muestral,
• $S^2(n)$: varianza muestral,
• $g$: precisión relativa deseada,
• $t$: valor de $t$ de Student con $n-1$ grados de libertad.

---

✅ Ejemplo 1: Cuando el número de réplicas realizadas es suficiente

Simulamos 10 réplicas y obtenemos:

• $\bar{X}(10)=4.5$
• $S^2(10)=0.36$
• $g=0.10$, $\alpha =0.10\Rightarrow t_{9,0.95}\approx 1.833$

$$n_r^{\ast }(0.10)={\left(\frac{1.833\cdot \sqrt{0.36}}{0.10\cdot 4.5}\right)}^2={\left(\frac{1.0998}{0.45}\right)}^2=5.97$$

🔍 Como hicimos 10 réplicas y necesitamos aproximadamente 6, ya cumplimos con la precisión deseada. ¡No se requieren más réplicas!

---

⚠️ Ejemplo 2: Cuando se necesitan más réplicas

Mismos datos pero mayor varianza:

• $S^2(10)=1.00$

$$n_r^{\ast }={\left(\frac{1.833\cdot \sqrt{1.00}}{0.10\cdot 4.5}\right)}^2={\left(\frac{1.833}{0.45}\right)}^2=16.6$$

➡️ Necesitamos 17 réplicas, pero solo hicimos 10.

Conclusión: La varianza fue alta y necesitamos seguir simulando.

---

Método secuencial

Si no sabemos cuántas réplicas se necesitan desde el inicio, podemos usar un procedimiento secuencial:

1. Comenzamos con al menos 10 réplicas.
2. Tras cada réplica nueva, recalculamos:
   • Media $\bar{X}(n)$,
   • Varianza $S^2(n)$,
   • Valor de $n_r^{\ast }$.
3. Parar cuando $n\ge n_r^{\ast }$

✔️ Ventaja: Evita hacer más réplicas de las necesarias.

📉 Desventaja: Puede requerir muchas réplicas si la varianza es alta.

---

Estimación de proporciones

(Ejemplo 9.16) Este ejemplo extiende el análisis de desempeño más allá de la media, al estimar una proporción: la fracción de clientes que esperan menos de 5 minutos en ser atendidos.

Tomando los datos de las mismas 10 réplicas utilizadas en el ejemplo anterior (ver Tabla 9.1), se desea calcular la proporción promedio de clientes que cumplieron con ese criterio en cada réplica, y construir un intervalo de confianza del 90%.

---

En cada réplica, se calcula la proporción de clientes cuyo tiempo de espera $Y_i$ se encuentra en el intervalo $[0,5)$ minutos, es decir:

$$X_j=\frac{1}{N_j}\sum _{i=1}^{N_j}{I}_i(0,5)$$

donde:

• $N_j$ es el número de clientes atendidos en la réplica $j$,
• $I_i(0,5)$ es una variable indicadora que vale 1 si el tiempo de espera del cliente $i$ está entre 0 y 5 minutos, y 0 si no.

---

A partir de los valores de $X_j$ en las 10 réplicas, se obtiene:

• Media muestral:

  $\bar{X}(10)=0.853$

• Varianza muestral:

  $S^2(10)=0.004$

---

Usando un valor $t_{9,0.95}=1.833$ (para un intervalo del 90% con 9 grados de libertad), el error estándar es:

$$\sqrt{\frac{0.004}{10}}=0.063$$

y el margen de error:

$$1.833\cdot 0.063\approx 0.12$$

Intervalo de confianza del 90% para la proporción:

$$0.853\pm 0.12=[0.733,0.973]$$

---

Interpretación

Con un 90% de confianza, se estima que entre el 73.3% y el 97.3% de los clientes esperaron menos de 5 minutos en ser atendidos. Este tipo de análisis permite evaluar el servicio desde una perspectiva más enfocada en la experiencia del cliente, y complementa el uso de la media al capturar la distribución del desempeño.

---

Estimación de otras medidas de desempeño

(Ejemplo 9.20) Considere nuevamente el Ejemplo 9.1 :

• Tasa de llegada: $\lambda =1$ cliente por minuto y
• Tasa de servicio: $\mu =0.25$ clientes por minuto por servidor.
• Numero de cajeros: $c=5$

La capacidad total del sistema es de:

$5\cdot \mu =5\cdot 0.25=1.25\text{ clientes por minuto}$ Esto implica un factor de utilización del sistema de:

$\rho =\frac{\lambda }{5\cdot \mu }=\frac{1}{5\cdot 0.25}=0.8$

Bajo este escenario se comparan dos políticas de atención a clientes:

• En la Política A, los clientes se forman en colas separadas, una por cada servidor.
• En la Política B, todos los clientes hacen una sola cola común y el primero en la fila es atendido por el siguiente servidor disponible.

Al realizar una simulación de ambas políticas, se observa que el tiempo de espera promedio diario de los clientes (es decir, la media) es muy similar en ambos casos. Sin embargo, al analizar con más detalle los resultados, se descubre que en la Política A hay una mayor proporción de clientes que experimentan tiempos de espera excesivos, lo cual no se refleja en la media.

---

---

---

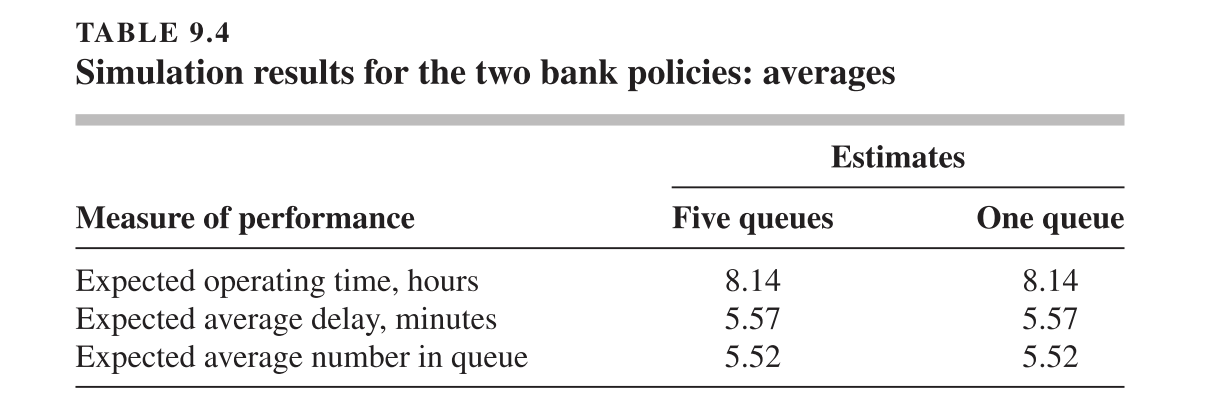
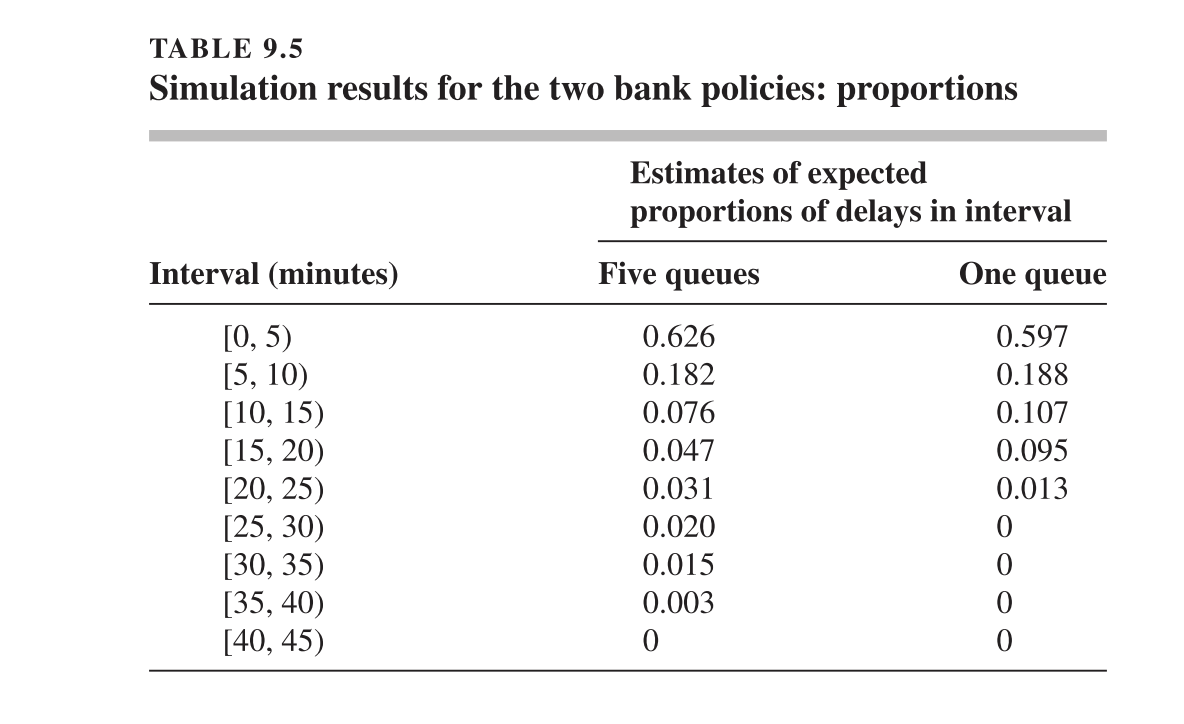
Por ejemplo, bajo la política de múltiples colas, una mayor proporción de clientes experimenta tiempos de espera elevados, lo cual no se refleja en la media. En contraste, la política de una sola cola produce un sistema más balanceado, con menos variabilidad en la experiencia de los clientes.

---

Este ejemplo demuestra que en muchas situaciones no basta con comparar únicamente las medias de desempeño, ya que pueden ocultar información relevante sobre la distribución de los resultados. Para una evaluación más completa, es útil estimar otras métricas como:

• Proporciones, por ejemplo: clientes que esperaron más de 5 minutos,
• Cuantiles, como el percentil 90 del tiempo de espera,
• Varianza o desviación estándar de los resultados,
• O integrales como el número promedio de clientes en cola durante el día.

---

Así, el análisis de salida se vuelve más robusto y útil para tomar decisiones informadas, considerando no solo los promedios, sino también la variabilidad y las experiencias extremas dentro del sistema simulado.

---

Bibliografia

Law, A. M. (2015). Simulation Modeling and Analysis (5th ed.). McGraw-Hill. Capítulo 9, pp. 429–509.

---

🎓 Ejercicio de simulación: Comparación de políticas de atención en una clínica

🎯 Objetivo del ejercicio:

Simular un sistema de colas con dos políticas de atención diferentes, y comparar los siguientes indicadores mediante 10 réplicas por política:

• Tiempo promedio de espera por paciente
• Tamaño promedio de la cola
• Proporción de pacientes que esperaron más de 10 minutos

---

🏥 Descripción del sistema: Clínica de consultas médicas

Una clínica atiende pacientes que llegan aleatoriamente y son atendidos por doctores. El sistema puede operar bajo dos políticas:

🔁 Política A: Un doctor por fila (múltiples colas)

• Hay 3 doctores.
• Cada uno tiene su propia cola independiente.
• El paciente elige una cola al azar al llegar.

🔁 Política B: Una sola cola común (FIFO global)

• Hay 3 doctores.
• Todos los pacientes hacen una sola cola compartida.
• El primer paciente en la cola es atendido por el siguiente doctor libre.

---

⚙️ Parámetros comunes para ambas políticas:

• Llegadas: Distribución exponencial, media = 3 minutos.

• Tiempos de servicio: Exponencial, media = 8 minutos.

• Horario de atención: 6 horas (360 minutos).

• Condición de terminación:

  La clínica cierra la entrada de nuevos pacientes después de los 360 minutos,
  pero todos los pacientes que hayan llegado antes del cierre deben ser atendidos.
  La simulación termina cuando se atiende al último paciente que llegó antes del cierre.

• Condición inicial: sistema vacío al inicio.

---

📋 Tareas del estudiante:

1. Simular cada política por separado usando CloudES o simulador equivalente.

2. Hacer 10 réplicas independientes para cada política.

3. En cada réplica, registrar:

   • Tiempo promedio de espera,
   • Longitud promedio de la cola,
   • Proporción de pacientes que esperaron más de 10 minutos.

4. Para cada métrica:

   • Calcular la media muestral y su intervalo de confianza del 90%,
   • Calcular la proporción muestral y su intervalo de confianza,
   • Comparar entre políticas.

---

📊 Análisis esperado:

• ¿Cuál política genera menor tiempo de espera promedio?
• ¿Cuál tiene menor tamaño de cola promedio?
• ¿Cuál es más justa en cuanto a distribución de tiempos de espera?
• ¿Hay una política claramente superior, o depende de la métrica?

---

📌 Formato sugerido para presentación de resultados:

Política	Réplica	Espera promedio	Cola promedio	% espera > 10 min
A	1	14.2 min	4.1	58%
B	1	10.5 min	2.9	40%
…	…	…	…	…